FUNGSI & GRAFIK

FUNGSI & GRAFIK

 

Grafik Persamaan

 

            Grafik suatu persamaan dalam x dan y terdiri atas titik-titik di bidang yang koordinat-koordinat (x,y)-nya memenuhi persamaan yakni, membuat suatu identitas yang benar.
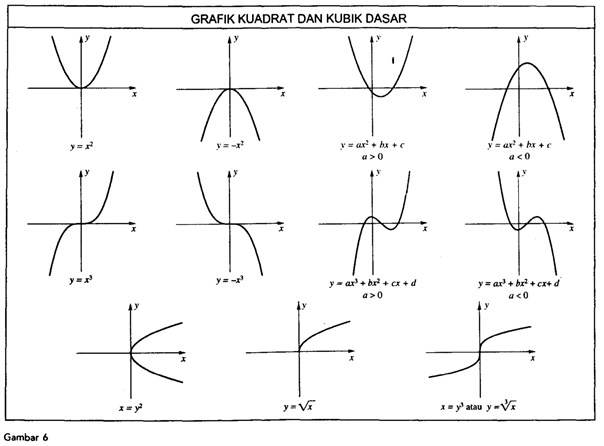
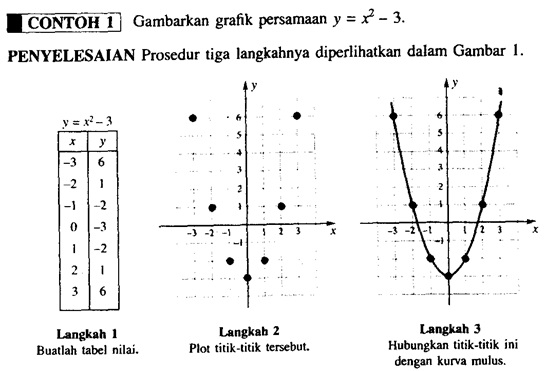
Prosedur Penggambaran Grafik Untuk menggambarkan suatu persamaan, misalnya y = 〖2x〗^3 - x + 19, kita dapat mengikuti prosedur tiga langkah sederhana:
Langkah 1: Dapatkan koordinat-koordinat beberapa titik yang memenuhi persamaan.
Langkah 2: Plotlah titik-titik tersebut pada bidang.
Langkah 3: Hubungkan titik-titik tersebut dengan sebuah kurva mulus.  

Fungsi dan Grafiknya

 
Definisi   
sebuah fungsi f adaIah suatu aturan korespondensi yang menghubungkan tiap obyek x dalam satu himpunan, yang disebut daerah asal (domain), dengan sebuah nilai tunggal f(x) dari suatu himpunan kedua. Himpunan nilal yang diperoleh secara
demikian disebut daerah hasil (range) fungsi.


Daerah asal dan daerah hasil untuk fungsi f dan g, diperlihatkan dalam tabel berikut.




0.6. Operasi pada Fungsi



Dengan asumsi bahwa f dan g mempunyai daerah asal alami, kita akan memperoleh:

Menyelesaikan Persamaan dan Pertidaksamaan Nilai Mutlak

Menyelesaikan Persamaan dan Pertidaksamaan Nilai Mutlak

Menyelesaikan Persamaan Mutlak

Nilai mutlak suatu bilangan dapat diartikan jarak antara bilangan tersebut dari titik nol(0). Dengan demikian jarak selalu bernilai positif.
Misalnya:
Parhatikan garis bilangan berikut.

Jarak angka 6 dari titik 0 adalah 6
Jarak angka -6 dari titik 0 adalah 6 
jarak angka -3 dari titik 0 adalah 3
Jarak angka 3 dari titik0 adalah 3.

Dari penjelesan di atas memang tampak bahwa nilai mutlak suatu bilangan selalu bernilai positif. 
Berkaitan dengan menentukan nilai mutlak suatu bilangan, maka muncullah tanda mutlak. Tanda mutlak disimbolkan dengan  garis 2 ditepi suatu bilangan atau bentuk aljabar.
Misalnya seperti berikut.

Secara umum, bentuk persamaan nilai mutlak dapat dimaknai seperti berikut.

Jika kita mempunyai persamaan dalam bentuk aljabar, maka dapat dimaknai sebagai berikut.

Jadi, bentuk dasar di atas dpat digunakan untuk membantu menyelesaikan persamaan mutlak.
Lebih jelasnya perhatikan contoh-contoh berikut.

Contoh
Tentukan himpunan penyelesaian dari persamaan nilai Mutlak di bawah ini.

Jawaban:
Bentuk-Bentuk persamaan nilai mutlak di atas dapat diselesaikan sebagai berikut. Pada prinsipnya, langkah langkah penyelesaian nilai mutlak diusahakan bentuk mutlak berada di ruas kiri. 
1. Pada bentuk ini ada dua penyelesaian.
   (*) x + 5 = 3  , maka  x = 3 - 5 = -2
   (**) x + 5 = -3, maka x = -3 - 5 = -8
  Jadi, himpunan penyelesaiannya adalah {-2, -8}

2.  Pada bentuk ini ada dua penyelesaian.
   (*) 2x + 3 = 5  , maka  2x = 5 - 3
                                       2x = 2  <==>  x = 1
   (**) 2x + 3 = -5  , maka  2x = -5 -3
                                         2x = -8  <==> x = -4
  Jadi, himpunan penyelesaiannya adalah {-4, 1}

3. Perhatikan bentuk aljabar di dalam tanda mutlak, yaitu x+1. Penyelesaian persamaan nilai mutlak ini juga dibagi menjadi dua bagian.
Bagian pertama untuk batasan x+1>= 0 atau x >= -1

Bagian kedua untuk batasan x+1< 0 atau x < -1
Mari kita selesaikan.
(*) untuk x >=-1
     Persamaan mutlak dapat ditulis:
    (x + 1) + 2x = 7
                   3x = 7 - 1
                   3x = 6
                     x = 2 (terpenuhi, karena batasan >= -1)

(**) untuk x < -1
     Persamaan mutlak dapat ditulis:
    -(x + 1) + 2x = 7
        -x - 1 + 2x = 7
                      x = 7 + 1                
                      x = 8 (tidak terpenuhi, karena batasan < -1)

Jadi, Himpunan penyelesaiannya adalah {2}.

 4. 
Perhatikan bentuk aljabar di dalam tanda mutlak, yaitu 3x + 4. Penyelesaian persamaan nilai mutlak ini juga dibagi menjadi dua bagian.
Bagian pertama untuk batasan 3x+4>= 0 atau x >= -4/3

Bagian kedua untuk batasan 3x+4< 0 atau x < -4/3
Mari kita selesaikan.
(*) untuk x >=-4/3
     Persamaan mutlak dapat ditulis:
    (3x + 4) = x - 8
        3x - x = -8 - 4
             2x =-12
               x = -6 (tidak terpenuhi, karena batasan >= -4/3)
(**) untuk x < -4/3
     Persamaan mutlak dapat ditulis:
    -(3x + 4) = x - 8
        -3x - 4 = x -8
         -3x - x = -8 + 4
              -4x = -4
                 x = 1 (tidak terpenuhi, karena batasan < -4/3)

Jadi, Tidak ada Himpunan penyelesaiannya.

Menyelesaikan Pertidaksamaan Nilai Mutlak
Menyelesaikan pertidaksamaan nilai mutlak caranya hampir sama dengan persamaan nilai mutlak. hanya saja berbeda sedikit pada tanda ketidaksamaannya. Langkah-langkah selanjutnya seperti menyelesaikan pertidaksamaan linear atau kuadrat satu variabel .
Pertidaksamaan  mutlak dapat digambarkan sebagai berikut.

Apabila fungsi di dalam nilai mutlak berbentuk ax + b maka pertidaksamaan nilai mutlak dapat diselesaikan seperti berikut.








Lebih jelasnya perhatikan contoh berikut ini.

Contoh
Tentukan himpunan penyelesaian dari Pertidaksamaan nilai mutlak berikut ini.

Jawaban
1. Cara menyelesaikan pertidaksamaan mutlak ini sebagai berikut.
    -9 < x+7 < 9
    -9 - 7 < x < 9 - 7
       -16 < x < 2
   Jadi, himpunan penyelesaiannya adalah { x/ -16 < x < 2}

2. Cara menyelesaikan pertidaksamaan mutlak ini dibagi menjadi dua bagian.
   (*) 2x - 1 >=  7
             2x  >=  7 + 1
             2x  >= 8
               x  >= 4

  (**) 2x - 1 <= -7
             2x   <= -7 + 1
             2x   <= -6
               x   <= -3
  
    Jadi, himpunan penyelesaiannya adalah { x/ x <= -3 atau x >= 4}

 3. Kalau dalam bentuk soal ini, langkah menyelesaikan pertidaksamaannya dengan mengkuadratkan kedua ruas.
perhatikan proses berikut ini.

(x + 3)² <= (2x – 3)²

(x + 3)² - (2x – 3)² <= 0

(x + 3 + 2x – 3) - (x + 3 – 2x + 3) <= 0 (ingat: a² – b² = (a+b)(a-b))

x (6 - x) <=0

Pembuat nol adalah x = 0 dan x = 6

Mari selidiki menggunakan garis bilangan

Oleh karena batasnya <= 0, maka penyelesaiannya adalah x <=0 atau x >=6.

Jadi, himpunan penyelesaiannya adalah {x/ x <= 0 atau x >= 6}.

Mari selidiki menggunakan garis bilangan

Oleh karena batasnya <= 0, maka penyelesaiannya adalah x <=0 atau x >=6.

Jadi, himpunan penyelesaiannya adalah {x/ x <= 0 atau x >= 6}.

4. Menyelesaikan pertidaksamaan nilai mutlak seperti ini lebih mudah menggunakan cara menjabarkan definisi.
Prinsipnya adalah batasan-batasan pada fungsi nilai mutlaknya.
Perhatikan pada 3x + 1 dan 2x + 4.

Dari batasan batasan itu maka dapat diperoleh batasan-batasan nilai penyelesaian seperti pada garis bilangan di bawah ini.

Dengan garis bilangan tersebut maka pengerjaanya dibagi menjadi 3 bagian daerah penyelesaian.
1. Untuk batasan x >= -1/3  ......(1)
   (3x + 1) - (2x + 4) < 10
          3x + 1 - 2x- 4 < 10
                         x- 3 < 10
                             x < 13 .......(2)

  Dari (1) dan (2) diperoleh irisan penyelesaian -1/3 <= x < 13

2. Untuk batasan -2<= x < -1/3  ......(1)
    -(3x + 1) - (2x + 4) < 10
          -3x - 1 - 2x - 4 < 10
                       -5x - 5 < 10
                             -5x < 15 
                               -x < 3
                             x > 3 .......(2)

  Dari (1) dan (2) tidak diperoleh irisan penyelesaian atau tidak ada penyelesaian.

3. Untuk batasan x < -2  ......(1)
   -(3x + 1) + (2x + 4) < 10
         -3x - 1 + 2x + 4 < 10
                        -x + 3 < 10
                             -x  < 7
                                x > -7 .......(2)

  Dari (1) dan (2) diperoleh irisan penyelesaian -7 < x < -2.

Jadi, himpunan penyelesaiannya adalah {x/ -1/3 <= x < 13 atau -7 < x < -2}.

Perhatikan contoh Pertidaksamaan mutlak lainnya berikut.

Sistem Bilangan Riil

Bilangan Riil

Bilangan riil atau sering disebut juga bilangan real dalam matematika menyatakan suatu bilangan yang dapat dibentuk menjadi desimal seperti 3.2678. Bilangan riil ini meliputi bilangan rasional yang direpresentasikan dalam bentuk desimal berakhir dan bilangan irasional yang direpresentasikan dalam bentuk desimal berulang. Untuk bilangan riil sendiri direpresentasikan sebagai salah satu titik pada garis bilangan.

Gambar disamping merupakan simbol yang sering digunakan untuk bilangan riil, sehingga kita akan lebih mudah untuk mengingatnya.

 Garis bilangan

            Setiap bilangan real berkorespondensi dengan satu dan hanya satu titik pada sebuah garis bilangan, yang disebut garis bilangan real.

 

 

 

Sifat-sifat Bilangan Riil :
1. Aksioma Medan



Bilangan Riil dalam operasi penjumlahan dan perkalian memenuhi aksioma berikut ini. Misalkan x dan y merupakan bilangan riil dimana x+y suatu operasi penjumlahan dan xy suatu operasi perkalian.

• Aksioma 1 ( hukum komutatif ) yaitu x+y=y+x dan xy=yx
• Aksioma 2 ( hukum asosiatif ) yaitu x+(y+z)=(x+y)+z dan x(yz)=(xy)z
• Aksioma 3 ( hukum distributif ) yaitu x(y+z)=xy+xz
• Aksioma 4 (eksistensi unsur identitas). Identitas untuk penjumlahan 0 dan untuk perkalian 1 yang menjadikan 0+x=x dan 1.x=x.
• Aksioma 5 (eksistensi negatif / invers) terhadap penjumlahan dimana x+y=0 maka dapat ditulis y=-x.
• Aksioma 6 (eksistensi resiprokal/invers) terhadap perkalian dimana xy=1 sehingga kita dapat melambangkan y=1/x

Himpunan yang memenuhi aksioma-aksioma diatas disebut medan, oleh karena itu aksioma-aksioma diatas disebut aksioma medan.
2. Aksioma Urutan
Disini kita akan mengasumsikan terdapat R+ yaitu bilangan riil positif, misalnya x dan y anggota R+, maka akan memenuhi aksioma :

• Aksioma 7 yaitu xy dan x+y anggota R+.
• Aksioma 8 yaitu untuk setiap x≠0 , x anggota R+ atau -x anggota R+, namun tidak mungkin keduanya sekaligus.
• Aksioma 9 yaitu 0 bukan merupakan anggota R+.

3. Aksioma Kelengkapan

• Aksioma 10 yaitu setiap anggota bilangan riil S yang memiliki batas atas memiliki supremum, yaitu ada bilangan riil B sehingga B=sup(S).

Contoh cara mengubah pecahan biasa kedesimal

contoh cara mengubah pecahan ke persen

contoh cara mengubah persen ke pecahan
 
 

    Sifat-sifat urutan bilangan real

Untuk setiap bilangan real a, b dan c berlaku sifat urutan berikut:

 

•          a < b = a + c < b + c

•          a < b = a - c < b – c

•          a < b, c > 0= = ac < bc

•          a < b, c < 0 = ac > bc

•          a > 0 =  

•          Jika a dan b bertanda sama maka