Limit Matematika dan Contoh Soal
Limit Matematika
– Tak terasa ujian nasional kurang dari sebulan lagi. Buat sobat
hitung, jangan lupa ikhtiar, doa, dan restu orang tua biar sukses ujian
nasionalnya. Siang ini rumushitung.com coba menyuguhkan materi buat me-refresh
ingatan sobat tentang materi limit matematika. Kami yakin soal limit
sudah hampir bisa dipastikan akan muncul dalam soal ujian nasional 2014,
entah itu soal limit biasa atau limit trigonometri.
Apa itu Limit Matematika?
Limit suatu fungsi f(x) untuk x mendekati suatu bilangan a adalah nilai pendekatan fungsi f(x) bilamana x mendekati a
ini berarti bahwa nilai dari fungsi f(x) mendekati M jika nilai x mendekati a biar lebih paham kita simak contoh berikut
Contoh 1Tentukan limit dari
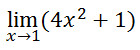
Jawab :
Untuk nilai x mendekati 1 maka (4x2+1) akan mendekati 4.12 + 1 = 5 sehingga nilai dari
Contoh 2
Tentukan nilai dari limit
Jawab
Misal sobat langsung memasukkan nili x = 1 ke dalam persamaan hasilnya tidak akan terdefinisi karena bilangan pembagi ketemu 0 (x-1). Akan tetapi bentuk di atas masih bisa disederhakan guna menghilangkan komponen pembagi yang bernilai nol yaitu
Misal sobat langsung memasukkan nili x = 1 ke dalam persamaan hasilnya tidak akan terdefinisi karena bilangan pembagi ketemu 0 (x-1). Akan tetapi bentuk di atas masih bisa disederhakan guna menghilangkan komponen pembagi yang bernilai nol yaitu
Cara Mengerjakan Limit Fungsi yang Tidak Terdefinisi
Adakalanya
penggantian niali x oleh a dalam lim f(x) x→a membuat f(x) punya nilai
yang tidak terdefinisi, atau f(a) menghasilkan bentuk 0/0, ∞/∞ atau 0.∞.
Jika terjadi hal tersebut solusinya adalah bentuk f(x) coba sobat
sederhanakan agar nilai limitnya dapat ditenntukan.
Limit Bentuk 0/0
Bentuk 0/0 kemungkinan timbul dalam
ketika sobat menemukan bentuk seperti itu coba untuk utak-utik fungsi tersebut hingga ada yang bisa dicoret. Jika itu bentuk persaman kuadrat sobat bisa coba memfaktorkan atau dengan cara asosiasi dan jangan lupakan ada aturan a2-b2 = (a+b) (a-b). Berikut contohnya
Bentuk ∞/∞
Bentuk limit ∞/∞ terjadi pada fungsi suku banyak (polinom) seperti
Contoh Soal
Coba sobat tentukan
Coba sobat tentukan
Jawab
Berikut rangkuman rumus cepat limit matematika bentuk ∞/∞
- Jika m<n maka L = 0
- Jika m=n maka L = a/p
- Jika m>n maka L = ∞
Bentuk Limit (∞-∞)
Bentuk (∞-∞) sering sekali muncul dalam ujian nasional.
Bentuk soalnya akan sangat beragam. Namun demikian, penyelesaiannya
tidak jauh-jauh dari penyederhanaan. Be creative, out of the box.
Berikut contoh soal yang kami ambil dari ujian nasional 2013.
Tentukan Limit
Jika
sobat masukkan x -> 1 maka bentuknya akan mmenjadi (∞-∞). Untuk
menghilangkan bentuk ∞-∞ kita sederhanakan bentuk tersebut menjadi
Sekian
dulu sobat belajar kita tentang limit matematika. Untuk limit
trigonometri akan kita sajikan pada postingan tersendiri. Selamat
belajar.
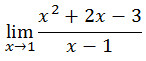
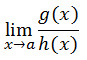
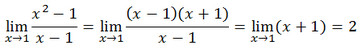
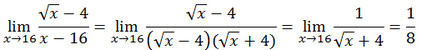
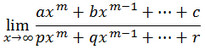
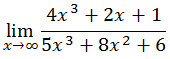
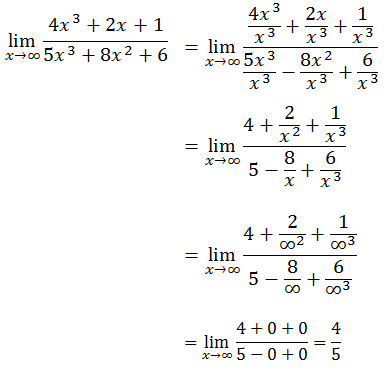
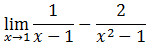
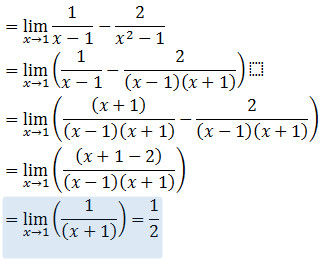


Tidak ada komentar:
Posting Komentar